Question

F(x)= x3 – 4x2-11x +30

Use the long division to find the remaining zeros given one of the zeros is 5.

Answer 1

The remaining zeros are 2 and -3.

Explanation:

Given cubic function:

`f(x)=x^3-4x^2-11x+30`

According to the factor theorem, if f(5) = 0 then (x - 5) must be a factor of the function f(x).

Therefore:

• Dividend: x³ - 4x² - 11x + 30
• Divisor: (x - 5)

Long division method

1. Divide the first term of the dividend by the first term of the divisor, and put that in the answer.
2. Multiply the divisor by that answer, put that below the dividend.
3. Subtract to create a new dividend.
4. Repeat.
5. The solution is the quotient plus the remainder divided by the divisor.

`\large \begin{array}{r}x^2+x-6\phantom{)}\\x-5{\overline{\smash{\big)}\,x^3-4x^2-11x+30\phantom{)}}}\\{-~\phantom{(}\underline{(x^3-5x^2)\phantom{-bbbbbbbb))}}\\x^2-11x+30\phantom{)}\\-~\phantom{()}\underline{(x^2-5x)\phantom{bbbbb..}}\\-6x+30\phantom{)}\\-~\phantom{()}\underline{(-6x+30)}\\0\phantom{)}\end{array}`

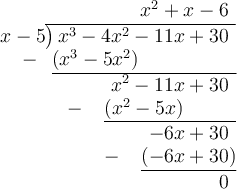
As the remainder is zero, the function can be written as:

`f(x)=(x-5)(x^2+x-6)`

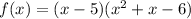
Factor the quadratic factor:

`\begin{aligned} \implies x^2+x-6&=x^2+3x-2x-6\\&=x(x+3)-2(x+3)\\&=(x-2)(x+3)\end{aligned}`

Therefore, the factored function is:

`f(x)=(x-5)(x-2)(x+3)`

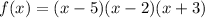
The zeros of a function can be found by setting each of the factors to zero:

`\implies x-5=0 \implies x=5`

`\implies x-2=0 \implies x=2`

`\implies x+3=0 \implies x=-3`

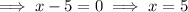
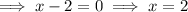
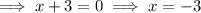
Therefore, given one of the zeros is 5, the remaining zeros are 2 and -3.