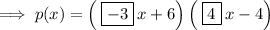Answer:
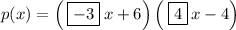
Explanation:
The x-intercepts are the points at which the curve crosses the x-axis.
From inspection of the given graph, the x-intercepts are:
As the parabola opens downwards, the leading coefficient is negative.

Therefore:
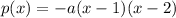
Expand:
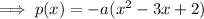
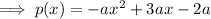
The y-intercept is the point at which the curve crosses the y-axis, so when x = 0. As the curve intersects the y-axis at y = -24:
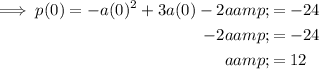
Therefore the equation in intercept form is:
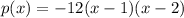
Rewrite -12 as 4 · -3:
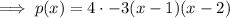
Multiply (x - 1) by 4 and (x - 2) by -3:
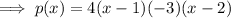
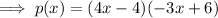
Applying the commutative property of multiplication:
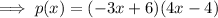
Compare with the given function: