Question

Given b is the midpoint of ac, find the length of bc if ab=x+6 and ac=5x-15

Answer 1

Given :-

• B is the midpoint of AC .
• AB = x + 6 and AC = 5x - 12 .

To find:-

• The length of BC .

Answer:-

Here we are given that B is midpoint of AC . So B divides AC into two equal halves AB and BC .

That is ,

`\implies (AC)/(2)= AB = BC`

`\implies AC = 2AB = 2BC`

Now we are here given that,

• AB = x + 6
• AC = 5x - 12

Since AB = BC , therefore;

`\implies BC = 5x -12`

Therefore , as ;

`\implies (AC)/(2)= BC`

So that;

`\implies 5x - 15 = 2( x + 6)\\`

`\implies 5x - 15 = 2x + 12\\`

`\implies 5x - 2x = 15+12`

`\implies 3x = 27`

`\implies x =(27)/(3)`

`\implies x = 9`

Now substitute this value in BC as ;

`\implies BC = x + 6`

`\implies BC = 9 + 6`

`\implies\underline{\underline{ BC = 15}}`

Hence the measure of BC is 15 .

and we are done!

Answer 2

The length of bc is 15 units.

Explanation:

The midpoint of a line segment is halfway between its two end points.

If b is the midpoint of ac, then ab + bc = ac and ab = bc.

Given:

• 
  `ab = x + 6`
• 
  `ac = 5x - 15`

Substitute the given expressions into the equation and solve for x.

`\begin{aligned}\implies ab+bc&=ac\\ab+ab&=ac\\2ab&=ac\\2(x+6)&=5x-15\\2x+12&=5x-15\\-3x&=-27\\x&=9\end{aligned}`

As ab = bc and ab = x + 6, then bc = x + 6.

Substitute the found value of x into the expression for bc.

`\begin{aligned}\implies bc&=x+6\\&=9+6\\&=15\end{aligned}`

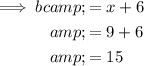
Therefore, the length of bc is 15 units.