Question

A water resources engineer is trying to run a cost-benefit analysis for a project. They need to first decide on the planning period (the benefits should be calculated over N years, and N should be determined). If N is too large, then the future benefits in those years (e.g. 70 years from now) will have a very low present value. Therefore, the engineer would like to cut off the planning period after a point when the present equivalent of benefits becomes less than 6.25% of that future benefit. If the interest rate is 8%, use the rule of 72 to determine the duration of the planning period (N).

Answer 1

N = 36 years

Step-by-step explanation:

Solution:

According to the 72 rule, present sum doubles in value, if the product of interest rate in percent and number of compounding period is 72.

So, We can say for every 9 years at 8 percent = 72 = present sum will be doubled.

Similarly, it will be doubled at 18 years., then 27 years, then 36 years and so on.

SO,

We need to find the P/F ratio, for the end of 0 years first.

Formula = (P/F, i, n) =
`(1 + i)^(-n)`

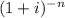
here,

i = 8%

n = 0 years.

P/F =
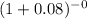`(1 + 0.08)^(-0)` (Anything power zero = 1)

So, similarly, calculate this P/F ratio for every 9 years till present equivalent of benefits becomes less than 6.25% of that future benefit.

find the P/F ratio, for the end of 9 years:

Formula = (P/F, i, n) =
`(1 + i)^(-n)`

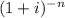
here,

i = 8%

n = 9 years.

P/F =
`(1 + 0.08)^(-9)`

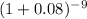
P/F = 0.50

Amount = 2x

find the P/F ratio, for the end of 18 years:

Formula = (P/F, i, n) =
`(1 + i)^(-n)`

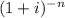
here,

i = 8%

n = 18 years.

P/F =
`(1 + 0.08)^(-18)`

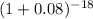
P/F = 0.25

Amount = 4x

find the P/F ratio, for the end of 27 years:

Formula = (P/F, i, n) =
`(1 + i)^(-n)`

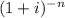
here,

i = 8%

n = 27 years.

P/F =
`(1 + 0.08)^(-27)`

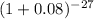
P/F = 0.13

Amount = 8x

find the P/F ratio, for the end of 36 years:

Formula = (P/F, i, n) =
`(1 + i)^(-n)`

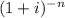
here,

i = 8%

n = 36 years.

P/F =
`(1 + 0.08)^(-36)`

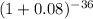
P/F = 0.06 = P/F ratio percentage = 6%

Amount = 16x

Hence, N = 36 years because it is the value nearest to 6.25% required

find the P/F ratio, for the end of 45 years:

Formula = (P/F, i, n) =
`(1 + i)^(-n)`

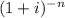
here,

i = 8%

n = 45 years.

P/F =
`(1 + 0.08)^(-45)`

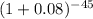
P/F = 0.03

Amount = 32x