Answer:
64 dimes and 34 quarters.
Explanation:
Let d represent the amount of dimes and q represent the amount of quarter Julie has.
She has in total 98 coins. Therefore:
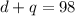
Each dime is worth 0.10 and each quarter is worth 0.25. Together, they are worth in total $14.90. Therefore:
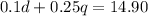
We have a system of equations. We can solve this using substitution.
First, we can multiply the second equation by 100 to simplify. So:
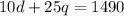
From the first equation, we can subtract q from both sides:
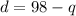
Substitute this into the second equation:
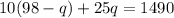
Distribute:
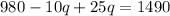
Combine like term:

Subtract:
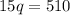
Therefore:
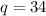
So, Julie has 34 quarters.
Returning to our first equation:
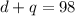
Substitute:
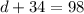
Therefore:
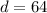
Thus, Julie has 64 dimes and 34 quarters.