Answer:
a) Compounded Annually = $9671.41
b) Compounded Monthly = $9691.51
c) Compounded Weekly = $9692.93
d) Compounded Daily = $9693.30
e) Compounded Continuously = $9693.36
Step-by-step explanation:
Solution:
This question is very simple. We just need to know the basic formula.
Data Given:
P = Principal Amount = $8000
i = interest rate = 2.4% annual
n = period or year = 8 years.
So, our basic formula is:
A = P
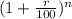
a) Compounded Annually.
A = P
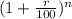
A = 8000
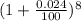
A = $9671.41
b) Compounded Monthly:
1 year = 12 months.
A = P
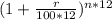
A = 8000
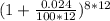
A = $9691.51
c) Compounded Weekly:
1 year = 52 weeks
A = P

A = 8000
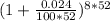
A = $9692.93
d) Compounded Daily:
1 year = 365 days
A = P
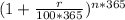
A = 8000
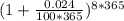
A = $9693.30
e) Compounded Continuously:
For this we have following formula:
A = P

A = P
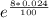
A = $9693.36