Answer:
Shortest side = 7 inches.
Medium side = 9 inches.
Longest side = 10 inches.
Explanation:
Let the shortest side be x.
Translating the word problem into an algebraic equation, we have;
Shortest side = x
Medium side = x + 2
Longest side = x + 3
The perimeter of a triangle is given by the addition of all its three (3) sides.
Mathematically, the perimeter of a triangle is given by the formula;
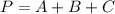
Substituting into the equation, we have;
26 = x + x + 2 + x + 3
26 = 3x + 5
3x = 26 - 5
3x = 21
x = 21/3
x = 7 inches.
Therefore, the length of the three sides are;
Shortest side = x = 7 inches.
Medium side = x + 2 = 7 + 2 = 9 inches.
Longest side = x + 3 = 7 + 3 = 10 inches.