Question

A constant torque of 3 Nm is applied to an unloaded motor at rest at time t = 0. The motor reaches a speed of 1,393 rpm in 4 s. Assuming the damping to be negligible, calculate the motor inertia in Nm·s2.

Answer 1

The moment of inertia of the motor is 0.0823 Newton-meter-square seconds.

Step-by-step explanation:

From Newton's Laws of Motion and Principle of Motion of D'Alembert, the net torque of a system (
`\tau`), measured in Newton-meters, is:

`\tau = I\cdot \alpha` (1)

Where:

`I` - Moment of inertia, measured in Newton-meter-square seconds.

`\alpha` - Angular acceleration, measured in radians per square second.

If motor have an uniform acceleration, then we can calculate acceleration by this formula:

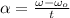`\alpha = (\omega - \omega_(o))/(t)` (2)

Where:

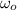`\omega_(o)` - Initial angular speed, measured in radians per second.

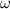`\omega` - Final angular speed, measured in radians per second.

`t` - Time, measured in seconds.

If we know that
`\tau = 3\,N\cdot m`,
`\omega_(o) = 0\,(rad)/(s )`,
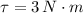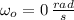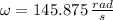`\omega = 145.875\,(rad)/(s)` and
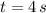`t = 4\,s`, then the moment of inertia of the motor is:

`\alpha = (145.875\,(rad)/(s)-0\,(rad)/(s))/(4\,s)`

`\alpha = 36.469\,(rad)/(s^(2))`

`I = (\tau)/(\alpha)`

`I = (3\,N\cdot m)/(36.469\,(rad)/(s^(2)) )`

`I = 0.0823\,N\cdot m\cdot s^(2)`

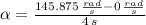
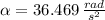
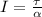
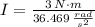
The moment of inertia of the motor is 0.0823 Newton-meter-square seconds.