Answer:
The proportion of this group that likes chocolate is 0.625.
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Likes sprinkles
Event B: Likes chocolate
25% of your friends who like Chocolate (C) also like sprinkles (S).
This means that

40% of your friends like sprinkles (S) topping.
This means that
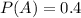
Of the friends who like sprinkles, what proportion of this group likes chocolate
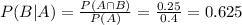
The proportion of this group that likes chocolate is 0.625.