Question

A pair of fair dice is cast. Let Edenote the event that the number landing uppermost on the first die is a 1 and let Fdenote the event that the sum of the numbers falling uppermost is 5. Determine whether Eand Fare independent events.Show your calculationsby describing the sample space, theeventsE and F, and combinations of these events as needed.

Answer 1

They are not independent

Explanation:

Given

E = Occurrence of 1 on first die

F = Sum of the uppermost occurrence in both die is 5

Required

Are E and F independent

First, we need to list the sample space of a roll of a die

`Event\ 1 = \{1,2,3,4,5,6\}`

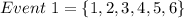
Next, we list out the sample space of F

`Event\ 2 = \{2,3,4,5,6,7,3,4,5,6,7,8,4,5,\`

`6,7,8,9,5,6,7,8,9,10,6,7,8,9,10,11,7,8,9,10,11,12\}`

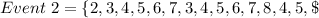
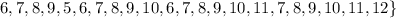
In (1): the sample space of E is:

`E = \{1\}`

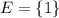
So:

`P(E) = (n(E))/(n(Event\ 1))`

`P(E) = (1)/(6)`

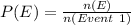
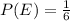
In (2): the sample space of F is:

`F = \{5,5,5,5\}`

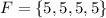
So:

`P(F) = (n(F))/(n(Event\ 2))`

`P(F) =(4)/(36)`

`P(F) =(1)/(9)`

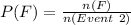
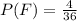
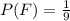
For E and F to be independent:

`P(E\ and\ F) = P(E) * P(F)`

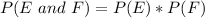
Substitute values for P(E) and P(F)

This gives:

`P(E\ and\ F) = (1)/(6) * (1)/(9)`

`P(E\ and\ F) = (1)/(54)`

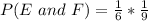
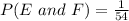
However, the actual value of P(E and F) is 0.

This is so because
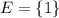`E = \{1\}` and
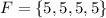`F = \{5,5,5,5\}` have 0 common elements:

So:

`P(E\ and\ F) = 0`

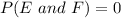
Compare
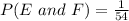`P(E\ and\ F) = (1)/(54)` and
`P(E\ and\ F) = 0`.

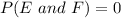These values are not equal.

Hence: the two events are not independent