Answer:
Answer: 8 (second choice)
Explanation:
Area of a Circle
Given a circle of radius r, the area is calculated by the formula:
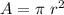
There are two circles in the diagram. The outer circle has a radius of r1=2x, thus its area is:

The interior circle has a radius of r2=6 cm, thus its area is:
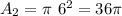
The shaded area is obtained by subtracting A1-A2:
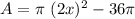
The value of the shaded area is given as 220π cm2. Equating:
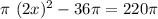
Dividing by π:
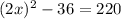
Adding 36:
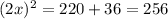
Taking square root:

Dividing by 2:
x = 8 cm
Answer: 8 (second choice)