Question

What is the solution to this system of equations

Answer 1

`(-1, -2)`

Explanation:

In this problem, we are asked to solve a system of equations given two equations each containing two variables: x and y. We can solve it using the substitution method.

First, we need to solve for a variable in terms of the other using one of the equations. I will solve for x in the first equation.

`4x-7y=10`

↓ add
`7y` to both sides

`4x=7y+10`

↓ divide both sides by 4

`x=(7y+10)/(4)`

Now that we have solved for x in terms of y, we can substitute the solved x-value into the bottom equation.

`3x + 2y = -7`

↓ substitute in solved x-value

`3\left((7y+10)/(4)\right) + 2y = -7`

↓ distribute 3

`(21y+30)/(4)\right) + 2y\left((4)/(4)\right) = -7\left((4)/(4)\right)`

↓ rewrite all terms as fractions over 4

`(21y+30 + 8y)/(4)\right)= -(28)/(4)`

↓ cancel denominators

`29y+30= -28`

↓ isolate y's

`29y = -28 - 30`

↓ simplify

`29y= -58`

↓ divide both sides by 29

`y = -2`

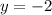
Now that we have solved exactly for y, we can solve for x using the substitution value we solved for earlier.

`x=(7y+10)/(4)`

↓ substitute in y-value

`x=(7(-2)+10)/(4)`

↓ simplify numerator

`x=(-14+10)/(4)`

`x=(-4)/(4)`

`x = -1`

Finally, we can put the solved x and y values into a Cartesian coordinate in the form (x, y).

`(-1, -2)`