Answer:

Explanation:
In this problem, we are asked to solve a system of equations given two equations each containing two variables: x and y. We can solve it using the substitution method.
First, we need to solve for a variable in terms of the other using one of the equations. I will solve for x in the first equation.

↓ add
 to both sides
to both sides

↓ divide both sides by 4

Now that we have solved for x in terms of y, we can substitute the solved x-value into the bottom equation.

↓ substitute in solved x-value

↓ distribute 3

↓ rewrite all terms as fractions over 4

↓ cancel denominators

↓ isolate y's

↓ simplify

↓ divide both sides by 29
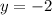
Now that we have solved exactly for y, we can solve for x using the substitution value we solved for earlier.

↓ substitute in y-value

↓ simplify numerator



Finally, we can put the solved x and y values into a Cartesian coordinate in the form (x, y).
