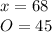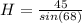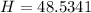Question

Your kite is stuck in a tree that is 45 feet tall. The angle your string makes with the ground is 68°. Rather than worrying about the kite, you decide to calculate how much string you have let out. Assuming the string is held tight and makes a straight line to the ground, how much string have you let out?

Answer 1

48.53 = 49 feet

Explanation:

sin 0 = opposite/hypotenuse

sin 68 = AB/AC = 45/x

x = 45/sin 68 = 45/0.9272 = 48.53

48.53 rounded = 49 feet

Answer 2

You have let out 48.5 feet of string

Explanation:

Attached is a sketch of the problem.

We can use SOH CAH TOA to find our answer.

In this acronym, O is the opposite side, A is the adjacent side, and H is the hypotenuse. S is for the SIN function. C is for the COS function. T is for the TAN function.

We can calculate the length of the string by using the SIN function.

So we can say the sine of angle x is the opposite side divided by the hypotenuse.

`sin(x)=(O)/(H)`

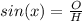
Lets solve for
`H`.

Multiply each term by
`H`.

`H*sin(x)=(O)/(H) *H`

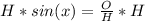
Simplify the right side by cancelling the common factor of
`H`.

`H*sin(x)=O`

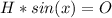
Divide both sides of the equation by
`sin(x)`.

`(H*sin(x))/(sin(x)) =(O)/(sin(x))`

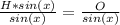
Simplify the right side by cancelling the common factor of
`sin(x)`.

`H=(O)/(sin(x))`

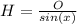
Now lets evaluate the length of the string.

In this example we are given

`x=68\\O=45`

`H=(45)/(sin(68))`

`H=48.5341`