Question

A small town has two local high schools. High School A currently has 850 students

and is projected to grow by 35 students each year. High School B currently has 700
students and is projected to grow by 60 students each year. Let A represent the
number of students in High School A int years, and let B represent the number of
students in High School B after t years. Write an equation for each situation, in terms
of t, and determine after how many years, t, the number of students in both high
schools would be the same.

Answer 1

For High School A, let
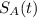`S_A(t)` denote the number of students after
`t` years. Define
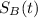`S_B(t)` analogously.

Then
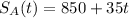`S_A(t) = 850 + 35t` and
`S_B(t) = 700 + 60t`.

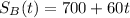After 6 years the number of students in both high schools would be the same.

Explanation:

For High School A, let
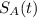`S_A(t)` denote the number of students after
`t` years. Define
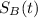`S_B(t)` analogously.

Since we start out at 850 students at High School A and it is growing by 35 students every year, we must have that
`S_A(t) = 850 + 35t`.

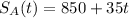Since we start out at 700 students at High School B and it is growing by 60 students every year, we must have that
`S_B(t) = 700 + 60t`.

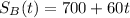Setting the two equations equal to each other, we see that
`850+35t=700+60t\\850-700=60t-35t\\25t=150\\t=6`

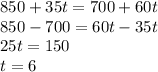
So after 6 years the number of students in both high schools would be the same.