Question

How do you solve the following word problem

A small radio transmitter broadcasts in a 49 mile radius. If you drive along a straight line from a city 67 miles north of the transmitter to a second city 63 miles east of the transmitter, during how much of the drive will you pick up a signal from the transmitter?


I must give the answer in miles and am unclear as to what equations to use and need details on what equations to use to get to the correct answer.

thanks for any help.

M

Answer 1

Explanation:

Let the transmitter be located at (0,0)

The equation for its effective coverage area will be a circle centered at (0,0) with a radius of 49.

So....the equation is

`x^2 + y^2 = 49^2`

`x^2 + y^2 = 2401`

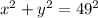
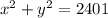
Let the point 67 miles north of the transmitter be (0, 67)

Let the point 63 miles east of the transmitter be (63, 0)

The line connecting these (the line of travel) will have a slope of

[67 - 0] / [ 0 - 63] = -67/63

The equation of this line will be: y = (-67/63)x + 67

The signal will be received between the points:

(21.681, 43.942) and (45.192, 18.938)

The distance between these points is

`√([ ( 45.192 - 21.681)^2 + ( 43.942 - 18.938)^2 ] ) = 34.322 miles` (1)

The distance between (0, 63) and (67, 0)

`√([ ( 63)^2 + ( 67)^2 ] )=91.97miles` (2)

So....you will receive the signal using (1)/ (2)

(34.322 / 91.97) x 100 ≈ 37% of the drive