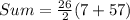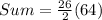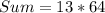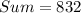Answer:
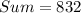
Explanation:
Given
See attachment
Required
Evaluate
The expression can be expressed as:
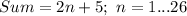
To do this, we make use of sum of n terms of an AP.
When n = 1
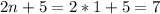 --- T1
--- T1
When n = 2
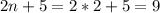 --- T2
--- T2
When n - 26
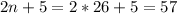 --- T26
--- T26
Next, we calculate d (common difference)
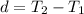

So, the sum is:
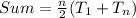
Let n = 26
So, we have:
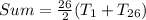
Substitute values for T1 and T26