Answer:
a = 18
Explanation:
The slopes of parallel lines are equal as

We know that the slope formula is
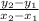 , where y2, x2, y1, and y2 are any two points.
, where y2, x2, y1, and y2 are any two points.
Thus, since the slopes are equal, we can use the slope formula to find the slopes of both lines and set them equal to each other to find a:

If we plug in a for any of the two lines, we see that the slope is -1/2
Line 1 w/ (a, 2) & (4, 9):

Line 2 w/ (3, 11) & (a+1, 3):
