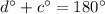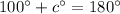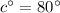Question

GEOMETRY:

I might just be slow but I don't understand what this question is asking at all. Can someone help?

Answer 1

`b = 90`

`d = 100`

`c = 80`

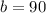
Explanation:

The problem is asking for the values of the variables
`b`,
`c`, and
`d` in the given parallelogram with angles
`d\textdegree`,
`c\textdegree`,
`(b-10)\textdegree`, and
`(b+10)\textdegree`.

To solve for these variables, we can construct three equations using the knowledge that any two adjacent angles of a parallelogram are supplementary (their measures add to 180º).

The first equation shows that the top two angles are supplementary:

`d\textdegree + c\textdegree = 180\textdegree`

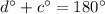
The second equation shows that the bottom two angles are supplementary:

`(b-10)\textdegree + (b+10)\textdegree = 180\textdegree`

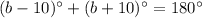
The third equations shows that the left two angles are supplementary:

`d\textdegree + (b-10)\textdegree = 180\textdegree`

First, we can solve for
`b` in the second equation using simple algebraic manipulation.

`(b-10)\textdegree + (b+10)\textdegree = 180\textdegree`

`(b+b)\textdegree + (10-10)\textdegree = 180\textdegree`

`2b\textdegree = 180\textdegree`

`b\textdegree = 90\textdegree`

`b = 90`

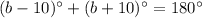
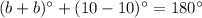
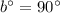
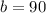
Using this
`b`-value, we can solve for
`d` by rewriting the third equation, plugging
`90` in for
`b`:

`d\textdegree + (b-10)\textdegree = 180\textdegree`

`d\textdegree + (90-10)\textdegree = 180\textdegree`

`d\textdegree + 80\textdegree = 180\textdegree`

`d\textdegree = 100\textdegree`

`d = 100`

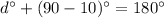
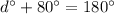
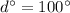
Finally, we can solve for
`c` in the first equation by plugging
`100` in for
`d`:

`d\textdegree + c\textdegree = 180\textdegree`

`100\textdegree + c\textdegree = 180\textdegree`

`c\textdegree = 80\textdegree`

`c = 80`