Answer:
Perpendicular line ⇒ 2x + 9y + 42 = 0
midpoint: (-1,1)
Explanation:
Let's find the coordinates of midpoint of AB
Here, from figure, A = (-3,-2), B = (1,4)
So midpoint:
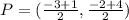
∴ P = (-1, 1)
Now, given straight line is x - 2y = -8(x-8)
⇒x - 2y = -8x+64
⇒9x - 2y - 64 = 0
Perpendicular line to 9x - 2y - 64 = 0 is 2x + 9y + k = 0
Perpendicular line passes though (6,-6)
Putting the values, we get
2(6) + 9(-6) + k = 0
⇒12 - 54 + k = 0
⇒k = 42
∴ Perpendicular line ⇒ 2x + 9y + 42 = 0