Answer: The two numbers are 1 and -7
1 minus -7 = 1 - (-7) = 1 + 7 = 8 .... difference
1 plus -7 = 1 + (-7) = -6 .... sum
===================================================
Step-by-step explanation:
Let x and y be the two numbers. Let's say that x > y. Meaning that x is the bigger value.
They have a difference of 8 tells us that
x-y = 8
since "difference" is the result of subtraction. The term "sum" means the result of addition. Having a sum of -6 tells us
x+y = -6
We have this system of equations
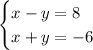
We can add the equations straight down. So we add the x terms to get x+x = 2x. The y terms add to -y+y = 0y = 0, so the y terms go away. The stuff on the right hand side adds to 8+(-6) = 2
After adding the equations straight down, we boil things down to the equation 2x = 2 which solves to x = 1, after dividing both sides by 2.
Then you'll use x = 1 to find y
x-y = 8
1-y = 8
-y = 8-1
-y = 7
y = -7
or
x+y = -6
1+y = -6
y = -6-1
y = -7
Regardless of what equation you pick, you should end up with the same y value. This helps confirm we have the correct x value.
Another way to check is to plug (x,y) = (1,-7) into both equations of the system. You should end up with true statements after simplifying fully.
So the two numbers are x = 1 and y = -7