Question

What is the inverse of the function
`y=x^(2) +4x+4`

Answer 1

y = 2 ± √x is the inverse but it's not a function. (See note below for additional info)

Explanation:

Given the quadratic function:

`\displaystyle{y = {x}^(2) + 4x + 4}`

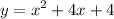
We can rewrite the function above using perfect square form:

`\displaystyle{y = {(x + 2)}^(2) }`

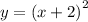
Finding an inverse, we swap the terms of x and y:

`\displaystyle{x = {(y + 2)}^(2) }`

Square root both sides, solving for y:

`\displaystyle{ √(x )= \sqrt{ {(y + 2)}^(2)} } \\ \\ \displaystyle √(x )= \left \\ \\ \displaystyle{ \pm √(x )= y + 2}`

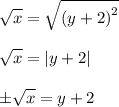
Subtract both sides by 2:

`\displaystyle{ \pm √(x ) - 2= y+ 2 - 2} \\ \\ \displaystyle{ \pm √(x ) - 2= y} \\ \\ \displaystyle{y = 2 \pm √(x) }`

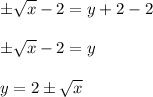
Therefore the inverse of y = x² + 4x + 4 is y = 2 ± √x.

Note: While it's possible to find the inverse of quadratic function, but the inverse version itself is not really a function. So if you want to go by definition or theorem, you can say there's no inverse function. Otherwise, the answer above is the solution.