Answer:

where P is the population, and t is the number of years after 500 BC.
b) 42,013,000
Explanation:

Define the variables:
- P = population
- t = time (in years)
The population in 500 BC is the initial value (when t = 0), therefore if the population was 310,000 in 500 BC:
If the population increases by 0.85% each year then the growth rate in decimal form is:
Therefore, the function that models the given scenario is:
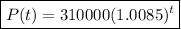
where P is the population, and t is the number of years after 500 BC.
To use the function to calculate the population in 80 AD, first calculate the number of years (value of t):
⇒ 80 AD - 500 BC = 580 years
Therefore, to find the population in 80 AD, substitute t = 580 into the function:
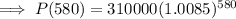
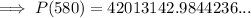
Therefore, the population in 80 AD is 42,013,000 (to the nearest thousand).