Question

What is the problem of this solving?!

Answer 1

This question can be solved primarily by L'Hospital Rule and the Product Rule.


`y= \lim_(x \to 0) (x^2cos(x)-sin^2(x))/(x^4)`

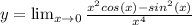
I) Product Rule and L'Hospital Rule:


`y= \lim_(x \to 0) ([2xcos(x)-x^2sin(x)]-2sin(x)cos(x))/(4x^3)`

II) Product Rule and L'Hospital Rule:


`y= \lim_(x \to 0) ([-2xsin(x)+2cos(x)]-[2xsin(x)+x^2cos(x)]-[2cos^2(x)-2sin^2(x)])/(12x^2) \\ y= \lim_(x \to 0) (2cos(x)-4xsin(x)-x^2cos(x)-2cos^2(x)+2sin^2(x))/(12x^2)`

III) Product Rule and L'Hospital Rule:


`]y= \alpha + \beta \\ \\ \alpha =\lim_(x \to 0) (-2sin(x)-[4sin(x)+4xcos(x)]-[2xcos(x)-x^2sin(x)])/(24x) \\ \beta = \lim_(x \to 0) (4sin(x)cos(x)+4sin(x)cos(x))/(24x) \\ \\ y = \lim_(x \to 0) (-6sin(x)-4xcos(x)-2xcos(x)+x^2sin(x)+8sin(x)cos(x))/(24x)`

IV) Product Rule and L'Hospital Rule:


`y = \phi + \varphi \\ \\ \phi = \lim_(x \to 0) (-6cos(x)-[-4xsin(x)+4cos(x)]-[2cos(x)-2xsin(x)])/(24x) \\ \varphi = \lim_(x \to 0) ([2xsin(x)+x^2cos(x)]+[8cos^2(x)-8sin(x)])/(24x)`

V) Using the Definition of Limit:


`y= (-6*1-4*1-2*1+8*1^2)/(24) \\ y= (-4)/(24) \\ \boxed {y= (-1)/(6) }`