This question can be solved primarily by L'Hospital Rule and the Product Rule.
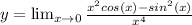
I) Product Rule and L'Hospital Rule:
![y= \lim_(x \to 0) ([2xcos(x)-x^2sin(x)]-2sin(x)cos(x))/(4x^3)](https://img.qammunity.org/2017/formulas/mathematics/high-school/kfxwv6sc6eaajun3v5l7rn9zzhhhnu82w3.png)
II) Product Rule and L'Hospital Rule:
![y= \lim_(x \to 0) ([-2xsin(x)+2cos(x)]-[2xsin(x)+x^2cos(x)]-[2cos^2(x)-2sin^2(x)])/(12x^2) \\ y= \lim_(x \to 0) (2cos(x)-4xsin(x)-x^2cos(x)-2cos^2(x)+2sin^2(x))/(12x^2)](https://img.qammunity.org/2017/formulas/mathematics/high-school/gmta286vppkpkw5r8ym551h94zxasrp9hd.png)
III) Product Rule and L'Hospital Rule:
![]y= \alpha + \beta \\ \\ \alpha =\lim_(x \to 0) (-2sin(x)-[4sin(x)+4xcos(x)]-[2xcos(x)-x^2sin(x)])/(24x) \\ \beta = \lim_(x \to 0) (4sin(x)cos(x)+4sin(x)cos(x))/(24x) \\ \\ y = \lim_(x \to 0) (-6sin(x)-4xcos(x)-2xcos(x)+x^2sin(x)+8sin(x)cos(x))/(24x)](https://img.qammunity.org/2017/formulas/mathematics/high-school/383s4tf3rswyt5f3qfusnayvvsqdmgkgvh.png)
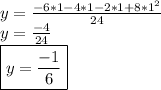
IV) Product Rule and L'Hospital Rule:
![y = \phi + \varphi \\ \\ \phi = \lim_(x \to 0) (-6cos(x)-[-4xsin(x)+4cos(x)]-[2cos(x)-2xsin(x)])/(24x) \\ \varphi = \lim_(x \to 0) ([2xsin(x)+x^2cos(x)]+[8cos^2(x)-8sin(x)])/(24x)](https://img.qammunity.org/2017/formulas/mathematics/high-school/hqfs2su4hzlo0vpvuzmsucctgapjmrmp47.png)
V) Using the Definition of Limit: