Question

Please please help me out

Given t4 = 187.5 and r = 2.5

a. Find the value of t1.

b. Write an explicit formula for this sequence.

c. Find the value of t18.

Answer 1

a)
`t_(1) = 12`

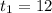
b) The explicit formula

`t_(n) = ar^(n-1) = 12(2.5)^(n-1)`

c) t₁₈ = 69,849,193.096

Explanation:

Step(i):-

Given that the geometric sequence

r = 2.5

Given the fourth term of the geometric sequence

`t_(4) = ar^(3) = 187.5`

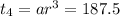
⇒ ar³ = 187.5

⇒ a (2.5)³ = 187.5

`a = (187.5)/((2.5)^(3) ) = 12`

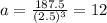
The explicit formula

`t_(n) = ar^(n-1) = 12(2.5)^(n-1)`

Step(ii):-

put n=1

`t_(1) = ar^(1-1) = 12(2.5)^(1-1) = 12 (2.5)^(0) = 12`

The
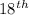`18^(th)` of the geometric sequence

`t_(18) = ar^(18-1) = a r^(17)`

`t_(18) = 12( 2.5)^(17)`

t₁₈ = 69,849,193.096

Final answer:-

a)
`t_(1) = 12`

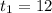
b) The explicit formula

`t_(n) = ar^(n-1) = 12(2.5)^(n-1)`

c) t₁₈ = 69,849,193.096