Answer:
a)
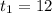
b) The explicit formula
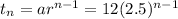
c) t₁₈ = 69,849,193.096
Explanation:
Step(i):-
Given that the geometric sequence
r = 2.5
Given the fourth term of the geometric sequence
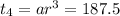
⇒ ar³ = 187.5
⇒ a (2.5)³ = 187.5
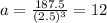
The explicit formula
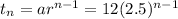
Step(ii):-
put n=1
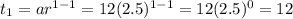
The
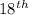 of the geometric sequence
of the geometric sequence
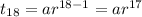
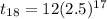
t₁₈ = 69,849,193.096
Final answer:-
a)
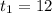
b) The explicit formula
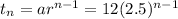
c) t₁₈ = 69,849,193.096