Question

HELP PLEASE !!! DUE IN 5 MINUTES !!!

Maria wants to buy shirts and pants for all her 18 cousins. She has $180 in total to buy shirts for $9 each and pants for $15 each. If Maria spends all her money how many shirts and pants can she buy? Set up a system of equations and show all your work. Use any method.

Answer 1

Answer: maria can buy 5 shirts and 2 pants

Explanation:

s = shirt p= pants

$180 total

per shirt = $9

per pant = $15

9(9x2) + (9x3) + (9x4) + (9x5) = $135 + 15(15x2) = $180

Answer 2

Try this suggested option:

Explanation:

1) if Maria has 180USD, then the maximum number of the pants she can buy is 180/15=12 (in this case number of the shirts is 0) and the maximum number of the shirts is 180/9=20 (and in this case number of the pants is 0).

If suppose the number of the pants is 'p' and of the shirts is 's', then

0 ≤p ≤12 - the 1st line in the system;

0 ≤s ≤20 - the 2d in the system.

2) according to the condition Maria has only 180 (USD), she can buy any number of 's' and 'p', this can be written as:

9s+15p = 180 - the 3d line in the system.

3) if to set up the required system, then (note, 's' and 'p' ∈Z):

`\left \{\begin{array}{ccc}9s+15p=180\\0\leq p\leq 12\\0\leq s\leq 20\end{array}\right`

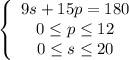
4) if to solve this system, only five pairs of s&p exist. They are:

0 shirts and 12 paints;

5 shirts and 9 paints;

10 shirts and 6 paints;

15 shirts and 3 paints;

20 shirts and 0 paints.

According to the condition Maria wants to buy s&p for all her 18 cousins, then the pair '15 shirts and 3 paints' is the best choice.

Answer: 15 shirts and 3 paints

PS. for more details see the attached graph, note the five pairs are marked with orange colour as points A, B, C, D and E.