Question

What type of conic section is given by the equation 4x^2+9y^2=36? What are its domain and range?

Answer 1

`4x^2+9y^2=36\\ \\ (4x^2)/(36)+(9y^2)/(36)=(36)/(36)\\ \\ \boxed{(x^2)/(9)+(y^2)/(4)=1}`

This is a equation of a ellipse (0,0) centered

Domais: {x∈R/-3≤x≤3}
Range:{y∈R/-2≤y≤2}

Answer 2

Ellipse

Domain:[-3,3]

Range:[-2,2]

Explanation:

We are given that an equation

`4x^2+9y^2=36`

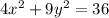
We have to find the type of conic section and find the domain and range of conic section.

Divide by 36 on both sides then, we get

`(x^2)/(9)+(y^2)/(4)=1`

`(x^2)/(3^2)+(y^2)/(2^2)=1`

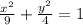
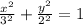
It is an equation of ellipse.

Substitute y=0 then , we get

`(x^2)/(9)=1`

`x^2=9`

`x=\pm 3`

Domain :[-3,3]

Substitute x=0 then we get

`(y^2)/(4)=1`

`y^2=4`

`y=\pm 2`

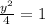
Range=[-2,2]