> 0
First, note that x is undefined at 5. / x ≠ 5
Second, replace the inequality sign with an equal sign so that we can solve it like a normal equation. / Your problem should look like:
= 0
Third, multiply both sides by x - 5. / Your problem should look like: 3x - 5 = 0
Forth, add 5 to both sides. / Your problem should look like: 3x = 5
Fifth, divide both sides by 3. / Your problem should look like: x =
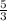Sixth, from the values of x above, we have these 3 intervals to test:
x <
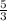
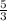
< x < 5
x > 5
Seventh, pick a test point for each interval.
1. For the interval x <
:
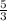
Let's pick x - 0. Then,
> 0
After simplifying, we get 1 > 0 which is true.
Keep this interval.
2. For the interval
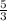
< x < 5:
Let's pick x = 2. Then,
> 0
After simplifying, we get -0.3333 > 0, which is false.
Drop this interval.
3. For the interval x > 5:
Let's pick x = 6. Then,
> 0
After simplifying, we get 13 > 0, which is ture.
Keep this interval.
Eighth, therefore, x <
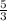
and x > 5
Answer: x <
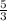
and x > 5