Question

Physical Science A ball is dropped from a height of 900 centimeters. The table shows the height of each bounce. The heights form a geometric sequence. How high does the ball bounce on the 5th bounce?​

Answer 1

the ball bounces i believe t

Explanation:

Answer 2

Since the heights form a geometric sequence, the height of the ball on the 5th bounce is 192.1 cm.

In Mathematics and Geometry, the nth term of any geometric sequence can be determined by using the following formula:

`a_n=a_1(r)^(n-1)`

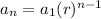
Where:

• 
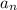  `a_n` is the nth term of any geometric sequence.
• r represents the common ratio.
• 
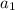  `a_1` represents the first term of any geometric sequence.

Based on the given sequence, we would determine the common ratio as follows;

Common ratio, r =
`(r_2)/(r_1)`

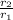
Common ratio, r = 560/800 = 392/560

Common ratio, r = 0.7.

Therefore, the nth term and the 9th term of this sequence are given by;

`a_n=a_1(r)^(n-1)\\\\a_n=800(0.7)^(n-1)\\\\a_5=800(0.7)^(5-1)\\\\a_5=800(0.7)^(4)\\\\a_5=192.08\approx192.1\;cm`

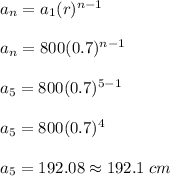
A ball is dropped from a height of 900 centimeters. The table shows the height of each bounce.

Bounce Height (cm)

1 800

2 560

3 392

The heights form a geometric sequence. How high does the ball bounce on the 5th bounce?​ Round your answer to the nearest tenth of a centimeter, if necessary.