Answer:
1.
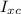 = 7.161458
= 7.161458
 in.⁴
in.⁴
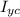 = 36.661458
= 36.661458
 in.⁴
in.⁴
Iₓ = 28.6458
 in.⁴
in.⁴
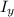 = 138.6548
= 138.6548
 in.⁴
in.⁴
2.
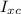 = 114.
= 114.
 in.⁴
in.⁴
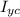 = 37.
= 37.
 in.⁴
in.⁴
Iₓ = 457.
 in.⁴
in.⁴
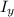 = 149.
= 149.
 in.⁴
in.⁴
3. The maximum deflection of the beam is 2.55552 inches
Step-by-step explanation:
1. The height of the beam having a rectangular cross section is h = 2.5 in.
The breadth of the beam, is = 5.5 in.
The moment of inertia of a rectangular beam through its centroid is given as follows;
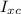 = b·h³/12 = 5.5 × 2.5³/12 = 1375/192 = 7.161458
= b·h³/12 = 5.5 × 2.5³/12 = 1375/192 = 7.161458

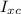 = 7.161458
= 7.161458
 in.⁴
in.⁴
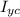 = h·b³/12 = 2.5 × 5.5³/12 = 6655/192 = 36.661458
= h·b³/12 = 2.5 × 5.5³/12 = 6655/192 = 36.661458

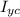 = 36.661458
= 36.661458
 in.⁴
in.⁴
The moment of inertia about the base is given as follows;
Iₓ = b·h³/3 = 5.5 × 2.5³/3 = 625/24 = 28.6458

Iₓ = 28.6458
 in.⁴
in.⁴
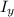 = h·b³/3 = 2.5 × 5.5³/3 = 6655/48= 138.6548
= h·b³/3 = 2.5 × 5.5³/3 = 6655/48= 138.6548

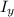 = 138.6548
= 138.6548
 in.⁴
in.⁴
2. The height of the beam having a rectangular cross section is h = 7 in.
The breadth of the beam, b = 4 in.
The moment of inertia of a rectangular beam through its centroid is given as follows;
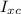 = b·h³/12 = 4 × 7³/12 = 114.
= b·h³/12 = 4 × 7³/12 = 114.

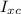 = 114.
= 114.
 in.⁴
in.⁴
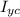 = h·b³/12 = 7 × 4³/12 = 37.
= h·b³/12 = 7 × 4³/12 = 37.

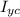 = 37.
= 37.
 in.⁴
in.⁴
The moment of inertia about the base is given as follows;
Iₓ = b·h³/3 = 4 × 7³/3 = 457.

Iₓ = 457.
 in.⁴
in.⁴
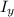 = h·b³/3 = 2.5 × 5.5³/3 = 149.
= h·b³/3 = 2.5 × 5.5³/3 = 149.

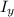 = 149.
= 149.
 in.⁴
in.⁴
3. The deflection,
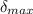 , of a simply supported beam having a point load at the center is given as follows;
, of a simply supported beam having a point load at the center is given as follows;
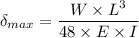
The given parameters of the beam are;
The length of the beam, L = 22 ft. = 264 in.
The applied load at the center, W = 750 lbs
The modulus of elasticity for Cedar = 10,000,000 psi
The height of the wood, h = 3 in.
The breadth of the wood, b = 5 in.
The moment of inertia of the wood,
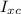 = b·h³/12 = 5 × 3³/12 = 11.25 in.⁴
= b·h³/12 = 5 × 3³/12 = 11.25 in.⁴
By plugging in the given values, we have;

The maximum deflection of the beam,
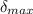 = 2.55552 inches
= 2.55552 inches