Question

the square of a certain whole number n is n^2. if 60 is a factor of n^2, it's possible that ? is not a factor of n^2. a)16 b)25 c)36 d)100

Answer 1

If 60 is a factor of n², then √60 is a factor of n. However, n is a whole number, so its factors are whole numbers.

Simplify √60:

`√(60)=√(4 * 15)=2√(15)`

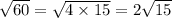
If 2√15 is a factor of a whole number n, then √15 must be another factor to make it a whole number.


`2√(15) * √(15)=2 * 15=2 * 3 * 5`

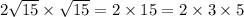
If 60 is a factor of n², then 2, 3, and 5 must be factors of n. The factors of n² are the squares of the factors of n, so 2, 2, 3, 3, 5, and 5 must be factors of n².

Now, if 2, 2, 3, 3, 5, and 5 are factors of n², then:
* 5×5=25 must also be its factor
* 2×2×3×3=36 must also be its factor
* 2×2×5×5=100 must also be its factor

Only 16 may not be a factor of n². The answer is A.