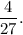Answer: The 10-th term of the sequence is
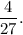
Step-by-step explanation: We are to find the 10-th term of a geometric sequence that has common ratio
 and fifth term is 36.
and fifth term is 36.
We know that the n-th term of a geometric sequence with first-term 'a' and common ratio 'r' is given by
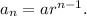
According to the given information, we have

and
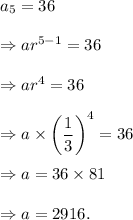
Therefore, the 10-th term of the sequence will be

Thus, the 10-th term of the sequence is