Answer:
The sum of the given geometric series is, 1
Explanation:
Geometric sequence states that a sequence of numbers that follows a pattern were the next term is found by multiplying by a constant called the common ratio (r).
The sum of the infinite terms of a geometric series is given by:
 ......[1] ;where
......[1] ;where
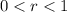
Given the series:
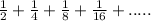
Since, this series is geometric series with constant term(r) =
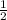
Since,
 ,
,
 and so on....
and so on....
Here, first term(a) =
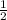
Substitute the values of a and r in [1] we get;
 where r =
where r =


or
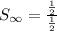
Simplify:

Therefore, the sum of the infinite geometric series is, 1