Question

In sunlight, a vertical stick 7 ft tall casts a shadow 3 ft long. At the same time a nearby tree casts a shadow 11 ft long. How tall is the tree? Round to the nearest tenth.

Answer 1

`look\ at\ the\ picture\\\\\Delta ABC\sim\Delta D EF\\\\(|ED|)/(|EF|)=(|AB|)/(|BC|)\\\\(|ED|)/(11)=(7)/(3)\ \ \ \ /\cdot11\\\\|ED|=(77)/(3)\\\\|ED|\approx25.7\ (ft)\leftarrow Answer`

Answer 2

25.7 feet.

Explanation:

Let x be the actual length of tree.

We have been given that in sunlight, a vertical stick 7 ft tall casts a shadow 3 ft long. We are asked to find the actual length of tree casting a 11 ft long shadow.

We will use proportions to solve our given problem.

`(x)/(11)=(7)/(3)`

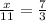
Upon multiplying both sides of our equation by 11, we will get:

`(x)/(11)*11=(7)/(3)*11`

`x=(77)/(3)`

`x=25.6666666\approx 25.7`

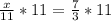
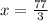
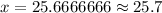
Therefore, the tree is 25.7 feet tall.