Answer:
448 half inch cubes can fit in the box.
Explanation:
A box is represented by a parallelepiped, whose volume (
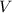 ), measured in cubic inches, is represented by the following formula:
), measured in cubic inches, is represented by the following formula:
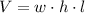 (1)
(1)
Where:
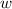 - Width, measured in inches.
- Width, measured in inches.
 - Height, measured in inches.
- Height, measured in inches.
 - Length, measured in inches.
- Length, measured in inches.
If we know that
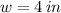 ,
,
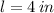 and
and
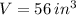 , then the height of the box is:
, then the height of the box is:
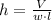
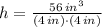
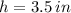
Given that box must be fitted by half inch cubes, the number of cubes per stage is:

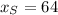
The number of stages within the parallelepiped is:
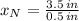
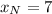
The total quantity of half inch cubes that can fit in the box is:
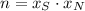
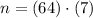
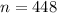
448 half inch cubes can fit in the box.