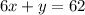Answer:
The equation of the line in standard form is:
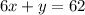
Explanation:
Given the points
Determining the slope between (10, 2) and (14, -22)

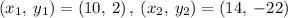
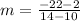
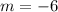
The point-slope form of the line equation is
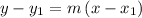
where
- m is the slope of the line
substituting the values m = -6 and the point (10, 2) in the point-slope form of the line equation
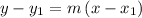

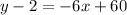
adding 2 to both sides

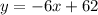
We can write the equation in the standard form such as
Ax + By = C
Thus,
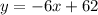
adding -6x to both sides
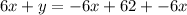
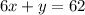
Therefore, the equation of the line in standard form is: