Question

Find the vertex of the function given below.

Answer 1

Option A i.e. (1, 0) is correct.

Explanation:

We know that graph of a Parabola illustrates a U-shaped curve.

The graph of Parabola has an important characteristic, it consists of an extreme point which is termed as 'vertex'.

When a parabola opens up, the vertex will be the lowest point on the Parabola graph.

When a parabola opens up, the vertex will be the lowest point on the Parabola graph. This lowest point is the minimum value of the parabola function.

Given the equation

y = x² - 2x + 1

From the given Parabola graph, it is clear that the parabola opens up.

Thus, the vertex will be the lowest point on the Parabola graph which is also the minimum value.

It is clear that the vertex of the parabola is located at (1, 0).

Therefore, the point (1, 0) is the vertex of the function.

SECOND METHOD:

Given the equation

y = x² - 2x + 1

The vertex of an up-down facing parabola of the form y = ax² + bx + c is

`x_v=-(b)/(2a)`

`a=1,\:b=-2,\:c=1`

`x_v=-(\left(-2\right))/(2\cdot \:1)`

`x_v=1`

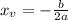
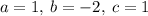
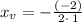
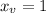
Plug on
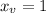`x_v=1` in the equation y = x² - 2x + 1 to find the
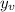`y_v` value

`\:y_v\:=\:x^(2) \:-\:2x\:+\:1`

`\:y_v\:=\:\left(1\right)^2\:-\:2\left(1\right)\:+\:1`

`y_v\:=1-2+1`

`y_v\:=0`

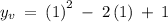
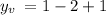
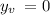
Therefore, the vertex is:

`\left(x_v,\:\:y_v\right)=\left(1,\:0\right)`

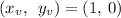
Hence, option A i.e. (1, 0) is correct.