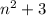Answer:
The nth term in the given sequence will be:
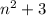
Explanation:
We are given a sequence as:
4,7,12,19,28,....
Let
 represents the nth term in the sequence.
represents the nth term in the sequence.
i.e.
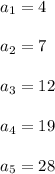
i.e. these terms could also be written as:
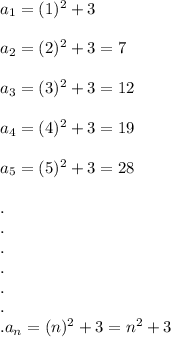
Hence the nth term in the given sequence will be: