Question

2cos^2(x)-5cos(x)+2=0

Answer 1

`x = (\pi)/(3) + 2n\pi \\ or\\ x=(-\pi)/(3) + 2n\pi`

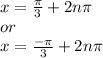
where "n" is an integer that belongs to Z.

Step-by-step explanation:

The equation given is:

2cos²(x) - 5cos(x) + 2 = 0

To factor this equation, we will use the quadratic formula shown in the attached image.

From the given equation:

a = 2

b = -5

c = 2

This means that:

either cos(x) =
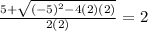`(5+√((-5)^2-4(2)(2)))/(2(2)) = 2` .......> This solution is rejected as the value of the cosine function lies between -1 and 1 only.

or cos(x) =
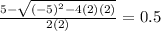`(5-√((-5)^2-4(2)(2)))/(2(2)) = 0.5` ......> This solution is accepted as it lies within -1 and 1

Now, using the inverse of the cosine, we can find that:

`x = (\pi)/(3) + 2n\pi \\ or\\ x=(-\pi)/(3) + 2n\pi`

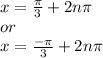
where "n" is an integer that belongs to Z.

Hope this helps :)

Answer 2

`2cos^2x-5cos+2=0\\\\cosx=t\in < -1;\ 1 >\\\\2t^2-5t+2=0\\\\a=2;\ b=-5;\ c=2\\\\\Delta=b^2-4ac;\ \Delta=(-5)^2-4\cdot2\cdot2=25-16=9\\\\t_1=(-b-\sqrt\Delta)/(2a);\ t_2=(-b+\sqrt\Delta)/(2a)\\\\t_1=(5-\sqrt9)/(2\cdot2)=(5-3)/(4)=(2)/(4)=(1)/(2)\in < -1;\ 1 >\\\\t_2=(5+\sqrt9)/(2\cdot2)=(5+3)/(4)=(8)/(4)=2\\otin < -1;\ 1 >`


`cosx=(1)/(2)\to x=(\pi)/(3)+2k\pi\ \vee\ x=-(\pi)/(3)+2k\pi\ \ \ (k\in\mathbb{Z})`