Question

An object's motion is described by the equation d = 4 sin(pi t ) . The displacement, d , is measured in meters. The time, t , is measured in seconds. Answer the following questions:

(a) What is the object's position at t = 0 ?
(b) What is the object's maximum displacement from its resting position?
(c) How much time is required for one oscillation?
(d) What is the frequency?

Answer 1

Explanation:

The given equation is:

`d=4sin({\pi}t)`, where d is the displacement. (1)

(A) The position of the object at t=0 is:

`d=4sin({\pi}(0))`

⇒
`d=4sin(0)`

⇒
`d=0`

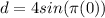
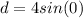
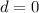
The object will be at rest at t=0.

(B) In order to find the maximum displacement from the resting position, we will differentiate the given displacement.

Thus, Differentiating with respect to t, we have

`d'=4cos({\pi}t)({\pi})`

⇒
`d'=4{\pi}cos({\pi}t)`

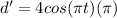
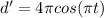
Now, d'=0

⇒
`4{\pi}cos({\pi}t)=0`

⇒
`cos{\pi}t=0`

⇒
`{\pi}t=\frac{{\pi}}{2}`

⇒
`t=(1)/(2)`

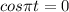
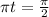
Substitute the value of t in equation (1), we get

⇒
`d=4sin({\pi}((1)/(2)))`

⇒
`d=4(1)`

⇒
`d=4m`

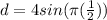
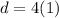
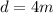
Thus, the maximum displacement from its resting position will be 4m.

(C) Time required for one oscillation is equal to the period which is equal to=
`(2\pi)/(|b|)=(2\pi)/(\pi)=2`

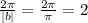
thus, time required for one oscillation will be 2 seconds.

(D) Frequency is nothing but the reciprocal of period that is
`(|b|)/(2\pi)=(\pi)/(2\pi)=(1)/(2)`

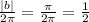
Thus, the frequency will be equal to
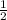`(1)/(2)`.

Answer 2

The equation of the motion is
d = 4 sin (π t)

a) When t = 0
d = 4 sin 0
d = 0

b) We take the derivative
4π cos πt = 0
t = 1/2
d = 4 sin π/2 = 4 meters

c) 1 second is required

d) The frequency is 1Hz