Question

For the function f(x) = (8-2x)2 ,find f-1 . Determine whether f-1 is a function.

A.
f-1(x) = ;f-1 is a function


B.
f -1 (x) = ; f-1 is not a function


C.
f-1(x) = ;f-1 is not a function


D.
f-1(x) = ; f-1 is a function

Answer 1

f(x) = (8-2x)2=y
let 's find the inverse is
(8-2x)2=y, (8-2x)=sqrt(y), and -2x=sqrt(y) -8, finally x= (-1/2)sqrt(y)+4
the inverse is f^-1(y)=(-1/2) √y + 4, when x=y

the inverse is f^-1(x)=(-1/2) √x + 4

A: f-1(x) = ;f-1 is a function

Answer 2

`y=(8\pm√(x))/(2)`

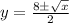
Step-by-step explanation:

We have been given with a function
`f(x)=(8-2x)^2`

We need to find
`f^(-1)`

when we find inverse of any function we intechange the variables we will get

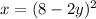`x=(8-2y)^2` after simplification we will get

`y=(8\pm√(x))/(2)`

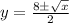
`f^(-1)` is not a function since, for each value of x there is two values of y.