Question

For an exponential function in the form of y=ab^x, if b is between 0 and 1, what happens to the graph of the function as x increases?

A.
The graph gets closer to the x-axis.
B.
The graph gets closer to the y-axis.
C.
The graph curves up away from the x-axis.
D.
The graph curves down away from the x-axis.

Answer 1

A.

The graph gets closer to the x-axis.

Explanation:

We are given an exponential function:

`y= ab^x`

Now we know that if a number lies between 0 and 1 and as we keep on increasing its power the number goes on decreasing and ultimately it tends to zero

Here, b lies between 0 and 1 so, as we keep on increasing the power of b it will tend to zero

i.e.
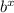`b^x` tends to zero

Hence,
`y=ab^x` tends to zero

i.e. The graph gets closer to the x-axis.

Hence, A is the correct option

Answer 2

The graph gets closer to the x-axis.