Question

Graph triangle ABC with vertices A(0,5) B(4,3) and C(2,-1) and it’s image after a reflection in the line y=2I starting by graphing triangle ABC just so you know!

Answer 1

A graph of triangle ABC and its image after a reflection in the line y = 2 is shown on the coordinate plane in the picture below.

In Mathematics and Euclidean Geometry, a reflection across the line y = k and y = 2 can be modeled by the following transformation rule:

(x, y) → (x, 2k - y)

(x, y) → (x, 4 - y)

By applying a reflection across the line y = 2 to the coordinates of the pre-image (triangle), we have the following image coordinates;

(x, y) → (x, 4 - y)

Point A (0, 5) → (0, 4 - 5) = A' (0, -1)

Point B (4, 3) → (4, 4 - 3) = B' (4, 1)

Point C (2, -1) → (2, 4 - (-1)) = C' (2, 5)

Answer 2

Given the triangle ABC, you can identify that the coordinates of its vertices are:

`\begin{gathered} A\mleft(0,5\mright) \\ B\mleft(4,3\mright) \\ C\mleft(2,-1\mright) \end{gathered}`

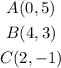
You know that it is reflected over the following line:

`y=2`

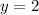
Notice that it has the form of a horizontal line. It intersects the y-axis at this point:

`(0,2)`

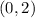
Knowing that you can graph the line. See the picture below:

By definition, when a figure is reflected over a line, the points of the Image (the figure obtained after the transformation) and the points of the Pre-Image (the original figure), have the same distance from the line of reflection.

Notice that:

- Point A is 3 units away from the line of reflection.

- Point B is 1 unit away from the line.

- Point C is 3 units away from the line.

See the picture attached:T

Therefore, the points of the Image will have this distance from the line of reflection:

- Point A' will be 3 units away from the line of reflection.

- Point B' will be 1 unit away from the line.

- Point C' will be 3 units away from the line.