Question

According to the Rational Root Theorem, which could be a factor of the polynomial f(x) = 60x4 + 86x3 – 46x2 – 43x + 8?

A. x – 6
B. 5x – 8
C. 6x – 1
D. 8x + 5

Answer 1

The correct option is C.

Explanation:

The given function is

`f(x)=60x^4+86x^3-46x^2-43x+8`

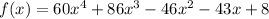
According to the rational root theorem, the potential root of the function are in the form of

`x=\pm \frac{\text{Factors of constant term}}{\text{Factors of leading coefficient}}`

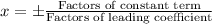
Here, constant term is 8 and leading coefficient is 60.

Factors of 8 are ±1, ±2, ±4, ±8 and factors of 60 are ±1,±2, ±3, ±4, ±5,±6,±10,±12,±15,±20,±30,±60.

So possible roots are,

`\pm 1, \pm (1)/(2), \pm (1)/(3), \pm (1)/(4), \pm (1)/(5), \pm (1)/(6),...`

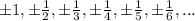
If f(c)=0, then (x-c) is a factor of f(x).

A. x – 6

`f(6)=60(6)^4+86(6)^3-46(6)^2-43(6)+8=94430`

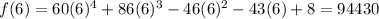
B. 5x – 8

`f((8)/(5))=60((8)/(5))^4+86((8)/(5))^3-46((8)/(5))^2-43((8)/(5))+8=566.912`

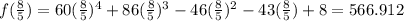
C. 6x – 1

`f((1)/(6))=60((1)/(6))^4+86((1)/(6))^3-46((1)/(6))^2-43((1)/(6))+8=0`

Since the value of f(x) is 0, therefore
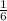`(1)/(6)` is a rational root and (6x-1) is a factor of given polynomial.

D. 8x + 5

`f((-5)/(8))=60((-5)/(8))^4+86((-5)/(8))^3-46((-5)/(8))^2-43((-5)/(8))+8=5.07`

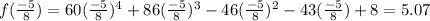
Therefore option C is correct.

Answer 2

If P(x) is a polynomial with integer coefficients and if is a zero of P(x) ( P( ) = 0 ), then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x) .

A. x – 6
60(6)^4 + 86(6)^3 – 46(6)^2 – 43(6) + 8 = 94430

B. 5x – 8
60(8/5)^4 + 86(8/5)^3 – 46(8/5)^2 – 43(8/5) + 8 = 566.912

C. 6x – 1
60(1/6)^4 + 86(1/6)^3 – 46(1/6)^2 – 43(1/6) + 8 = 0 -------> ANSWER

D. 8x + 5
60(-5/8)^4 + 86(-5/8)^3 – 46(-5/8)^2 – 43(-5/8) + 8 = 5.07