Answer:
A. The northern California study with a margin of error of 3.2%.
Explanation:
We know that,
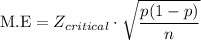
Where,
M.E = margin of error,
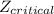 = z score of the confidence interval,
= z score of the confidence interval,
for 98% confidence interval
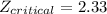
p = proportion,
n = sample size.
One study in northern California involved 1,000 patients; 74% of them experienced flu like symptoms during the month of December.
Putting the values,
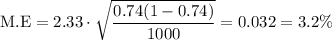
The other study, in southern California, involved 500 patients; 34% of them experienced flu like symptoms during the same month.
Putting the values,
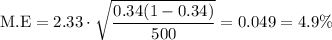
The smallest margin of error is 3.2% of the northern California study.