Question

Find S20 for the arithmetic series 8 + 16 + 24 + 32 +… super confused cause my options for answers are 1)1672 2)1688 3)1664 4)1680 shouldnt the answer be 160?

Answer 1

`S_(20) =1680`.

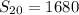Explanation:

Given : 8 + 16 + 24 + 32 +…..

To find : Find S20

Solution : We have given 8 + 16 + 24 + 32 +…..

First term = 8.

Common difference = 16 - 8= 8

24 -16 = 8.

Sum of n term (
`S_(n) =(n)/(2)[2 a+(n-1)d]`.

Where, a = first term , d =common difference .

For n = 20 , a = 8 , d = 8

`S_(20) =(20)/(2)[2*8+(20-1) 8]`.

`S_(20) =10[16+(19) 8]`.

`S_(20) =10[16+152]`.

`S_(20) =10[168]`.

`S_(20) =1680`.

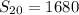Therefore,4)
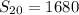`S_(20) =1680`.

Answer 2

First you have to find the 20th term... an = a1 + (n - 1)d n = 20 a1 = 8 d = 8 now lets sub... a20 = 8 + (20 - 1) * 8 a20 = 8 + 19 * 8 a20 = 8 + 152 a20 = 160 s20 is the sum of all the number till 20. so we will use the sum formula... sn = n(a1 + an) / 2 s20 = 20 (8 + 160) / 2 s20 = 20 (168) / 2 s20 = 3360/2 s20 = 1680 any questions ?