Answer:
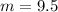 -- Unit rate of change
-- Unit rate of change
See attachment for graph
Explanation:
Given
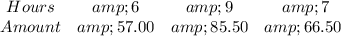
Solving (a): The unit rate of change.
This implies that we calculate the slope of the table.
This is calculated as:
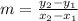
Where:
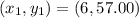
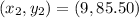
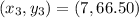
The equation becomes
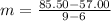
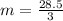
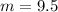
To graph the table, we need to determine the equation.
To do this, we make use of:

Substitute values for m, x3 and y3
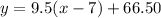
Open bracket
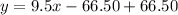
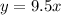
See attachment for graph