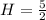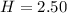Answer:
The equations are:
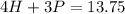
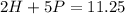
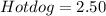
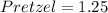
Explanation:
Let:
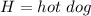
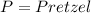
For Tina:
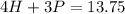
For Doug:
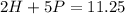
Solving for the price of both items:
We have:
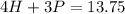 --- (1)
--- (1)
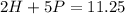 --- (2)
--- (2)
Multiply (2) by 2
2 * (
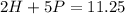 )
)
-------------------
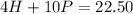 --- (3)
--- (3)
Subtract (3) from (1)
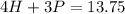
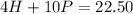
----------------------
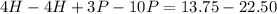

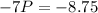
Solve for P
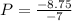
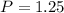
Substitute 1.25 for P in (2)
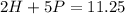

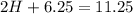
Collect Like Terms
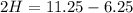
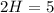
Solve for H